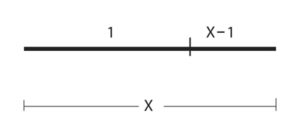1.6

(23-11-2018)

Le misure, le proporzioni, le simmetrie, traducono ai nostri sensi l’immagine che senza un tale controllo perderebbe il contatto diretto con chi ne ha ispirato il concetto e lo studio: l’uomo.

Le proporzioni, dunque, non solo si limitano a condurre in modo regolare la nostra vista e a indirizzarci verso la composizione dell’edificio ma sono un essenziale strumento per riuscire a controllare tutta la progettazione. Nel proseguo, parlando di proporzioni, si cercherà di dimostrare e mostrare come queste abbiano una valenza estetica, adombrate, purtroppo, come sono oggi dalla spettacolarizzazione del costruito che mette in sottordine l’armonia, quasi relegandola in antichi manoscritti, trasfigurando l’architettura, diventata bivacco di modaioli verticalisti e intreccisti.

Le proporzioni sono un mezzo, certamente non il fine così come definito in altre discussioni, ma senza di esse non sarebbe possibile costruire o realizzare un edificio architettonicamente accettabile, ne sfuggire alle sue regole ci porterebbe a risultati diversi da quelli generati dai disegni di un infante.

Perchè le proporzioni sono così importanti e fondamentali?

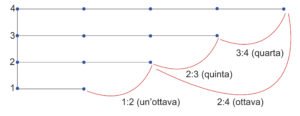
Esse trovano interesse nei più grandi studiosi di ogni tempo. Pensiamo solo a Pitagora; al matematico e filosofo si attribuisce la scoperta dell’interazione tra musica e  i numeri, resa evidente da semplici rapporti:  1:2 – 1:3 – 1:4 – 2:3 – 3:4. Come nascono questi rapporti?

Prendiamo, ad esempio, una corda che possa vibrare (tipo le corde di una chitarra) e stabiliamo “n” la sua misura; ebbene, nelle stesse condizioni di stato (ossia con la stessa tensione applicata) un’altra corda che misura la metà di questa, cioè “1/2 n”, vibrando avrà un suono di un’ottava più alto (diapason); abbiamo quindi definito il rapporto di 1:2.

Se invece la corda più corta è 2/3 di quella lunga la differenza di suono sarà di una quinta (diapente – 2:3 ), se è più corta nel rapporto di 3/4 la differenza di tono sarà di una quarta (diatessaron 3:4). Ecco come la musica si lega alla matematica e alla geometria.

Applicando questi semplici rapporti nella progettazione colleghiamo in modo sostanziale le varie arti,  dove l’architettura trasforma qualcosa di intangibile come la musica e la rende pietra.

Un collegamento tra le varie arti ben diverso da quello visto in un precedente articolo, operato dagli artisti del novecento dove l’incontro tra scultura e pittura, ad esempio, poteva essere affermato semplicemente tagliando a piacimento una tela.

Nell’analisi del noto  numero aureo troviamo altrettante ed interessanti deduzioni. Scoperto nell’antica Grecia e rappresentato con la lettera Φ [fi], ha trovato un ampio utilizzo in molte opere d’arte. Da dove proviene il numero aureo?

Cerchiamo di spiegarlo nel modo più semplice possibile attraverso dei passaggi algebrici: per prima cosa  poniamo una retta che misura X, che rappresenta un valore incognito, e dividiamo questa retta in due parti; una parte misura 1 e l’altra parte misura (x-1) così come è rappresentato nella immagine.

Questo rapporto tra il tutto e le parti è richiamato già dall’Alberti e da altri illustri architetti:    

Svolgiamo l’equazione e troviamo:   

Risulta un’equazione di secondo grado nella quale, delle due soluzioni prendiamo quella positiva:    

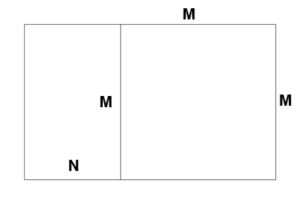
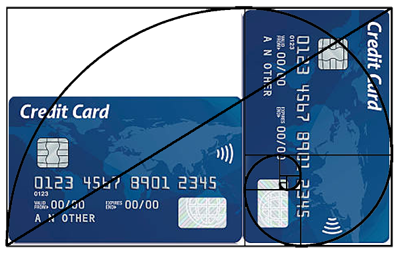
Questo è il rapporto che viene definito Aureo (Blog 1.6).  Il rapporto aureo nella geometria è ben esplicitato anche nei rettangoli; così un rettangolo aureo è definito tale quando il rapporto tra il lato maggiore e il lato minore è uguale a 1,61.

Se poi ad esso affianchiamo un quadrato, sempre di lato M, otteniamo un altro rettangolo aureo:    

Da ciò si deduce come si possano ottenere rettangoli aurei sempre più grandi.

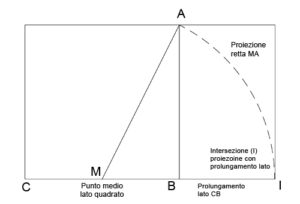
Un rettangolo aureo si può costruire anche partendo dal quadrato tramite un semplice compasso facendo perno nel punto medio di un lato tracciando la curva che parte da uno dei vertici opposti a questo; infine si proietta la retta andando a congiungere il prolungamento del lato sul quale abbiamo preso il punto medio. Il punto di intersezione ci da la misura del rettangolo aureo:

Alcune proprietà di Φ sono veramente interessanti, tra queste spicca la possibilità di costruire dei rettangoli aurei sempre più piccoli notando che il punto di intersezione tra le diagonali dei due rettangoli è sempre lo stesso e che le diagonali si incrociano in modo perpendicolare:

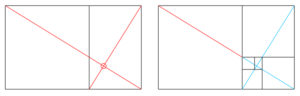
Questa successione porta a definire quella che viene chiamata spirale logaritmica:

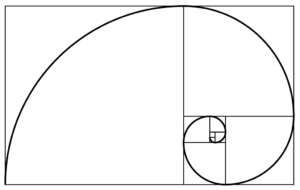
Nel 1876 il tedesco Gustav Theodor Fechner (1801-1887), l’inventore della psicometria eseguì un esperimento tra le persone lasciandole scegliere tra diversi tipi di rettangoli, indicando quello che più gli piaceva. Ebbene, la maggior parte scelse il rettangolo aureo. Egli teorizzò dopo molti studi statistici che un oggetto è considerato bello nella forma quando il rapporto tra la parte maggiore e quella minore è uguale al rapporto tra il maggiore e il tutto; questa a ben vedere è la definizione del numero aureo.

Senza aver fatto studi statistici, ritroviamo più o meno lo stesso concetto nel “De re aedificatoria” di Leon Battista Alberti al capitolo II del 6° libro così si esprime: ” Ad ogni modo, senza stare a dilungarci, definiremo la bellezza come l’armonia tra tutte le membra, nell’unità di cui fan parte, fondata sopra una legge precisa, per modo che non si possa aggiungere o togliere o cambiare nulla se non in peggio.”

Il maestro continua poi nel libro 9 inserendo la definizione di Concinnitas “…Giacchè tutto ciò che si manifesta in natura è regolato dalle norme della Concinnitas; e la natura non ha tendenza più forte che quella di far si che tutti i suoi prodotti riescano assolutamente perfetti. (0missis) La bellezza è accordo e armonia delle parti in relazione a un tutto al quale esse sono legate  secondo un determinato numero, delimitazione e collocazione, così come esige la Concinnitas, cioè la legge fondamentale e più esatta della natura. La quale Concinnitas è seguita quanto più possibile dall’architettura; essa è il mezzo onde quest’ultima consegue onore, pregio, autorità, valore”.

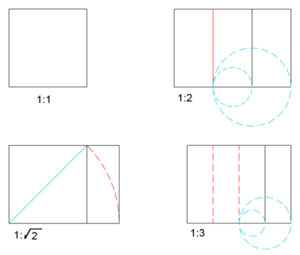
La ricerca di un controllo conferisce all’opera un aspetto armonico e ci permette di gestire in modo ottimale lo sviluppo progettuale, partendo per esempio, dalla semplice definizione di un quadrato. Da questo, in un crescendo definito da rapporti matematici e geometrici otteniamo degli spazi multipli così come descritti: 1:2 – 1:3 – 1:√2 (rapporto tra lato quadrato e sua diagonale) di 1:4 etc.

Dalle molteplici possibilità che un tale mezzo ci offre a noi rimane di riuscire nell’intento di realizzare quello che così ci descrive il Palladio all’inizio dei suoi quattro libri: “…La bellezza risentirà della bella forma, e dalla corrispondenza del tutto alle parti, delle parti fra loro, e di quelle al tutto; affinchè gli edifici abbiano da parere un intero e ben definito corpo, nel quale l’un membro all’altro collega, e tutte le membra siano necessarie a quello.”

Qui le parole sembrano far riferimento al corpo umano, tali da farci venire in mente l’uomo vitruviano ripreso da molti artisti, uno tra tutti quello più noto di Leonardo Da Vinci.

Ma già nel Medioevo la misura umana veniva usata come modello.

Nelle cattedrali francesi l’unità di misura era data da cinque aste, queste aste prendevano come riferimento il palmo della mano, le dita, la spanna, il piede e il gomito (tot. 5); e la somma di tutte le aste dava come risultato la lunghezza del braccio umano più il piede.

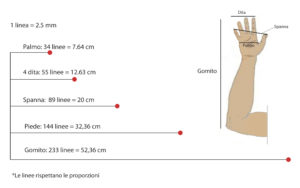
Tutte queste grandezze erano multipli di un’unica unità che veniva chiamata linea, corrispondente a circa 2,5 mm (2,247mm). Se adesso proviamo ad usare la successione di Fibonacci con la linea usata nel medioevo otteniamo un risultato sorprendente: 2,24 mm + 2,24 + 4,49 + 6,74 + 11,23 + 17,97 + 29,20 + 47,17 + 76,37 + 123,54 + 200….

Prima cosa notiamo che questa sommatoria ci porta in alcuni risultati i valori del palmo (76 mm) delle dita (123 mm) della spanna etc. Ed inoltre se andiamo a dividere l’ultimo risultato con quello che lo precede otteniamo il numero aureo Φ = 1,61 =>     

In pratica il corpo umano è basato sul rapporto aureo.

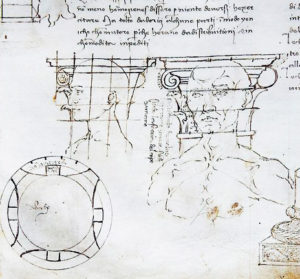D’altronde esempi di elementi architettonici definiti dalle misure del corpo umano li ritroviamo anche nei disegni sugli studi proporzionali di Francesco di Giorgio Martini  nel suo “Trattato di Architettura”; la volontà di un controllo per realizzare un’opera il più possibile armoniosa si lega ai dettami delle misure della natura in un rapporto che è si fisico ma che a mio giudizio va oltre la fisicità riprendendo e facendo confluire in questo tutti gli aspetti di una corretta progettazione.

Le proporzioni auree le ritroviamo anche in natura, nella vegetazione tra le foglie di un olmo dove il rapporto tra l’altezza e la larghezza delle foglio è 1,61 e in altre piante ancora.

Nel regno animale gli insetti tracciano una spirale aurea quando si avvicinano ad un punto luminoso; infatti se vogliamo accostarci ad un dato punto mantenendo lo stesso angolo di avvicinamento possiamo farlo solo in questo modo; d’altronde è quello che fanno i rapaci quando cacciano, così da avere sempre sotto controllo la preda.

Quello che è importante capire, a mio giudizio, è che tutta l’architettura, che sia moderna o del passato si sviluppa adottando  dei metodi di misurazione che prendono spunto dalla natura, proprio per cercare di ottenere quell’armonia che ci avvicina, in senso fisico e non solo, verso di essa. Un concetto che sarà approfondito e analizzato nella seconda parte del’articolo.